face: The plane figure between (at least 3) adjacent edges of a polyhedron where all the edges lie on the extended plane (from the plane figure) and all other edges lie on only one side of the plane.

face angle: The plane angle made between two edges in a polyhedral angle.

factor: Originally a positive integer that divides another given positive integer a whole number of times. This definition of factor has been extended to cover other mathematical objects which behave in similar ways, such as matrices and polynomials. In these cases the quotient no longer has to be a positive integer (since both division and integers are definitions that do not naturally apply to matrices anyway) in order for the divisor to qualify as a factor. In this sense, a factor (of a mathematical object) is best described as another mathematical object for which there is no remainder (alternatively, there is zero remainder) in writing the former mathematical object (which can be a number, polynomial or a matrix) as a multiple of the latter.

factorable: An mathematical object which can be considered as the result of combining (usually by multiplication) smaller (or simpler) constituent parts. e.g. A polynomial into products of linear expressions, a matrix into product of simpler matrices.

factor formulae: Also known as sum-to-product formulae. (Or product-to-sum formulae, if intended to use in the opposite way.)

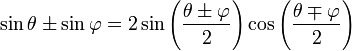
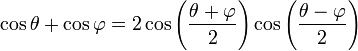
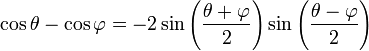
factorial: The factorial function is the function represented by an exclaimation mark. (e.g. 10! or n! ) Applied to a non-negative integer, it represents the product (multiplication) of all integers between the said number and 1 (inclusive). When the function is applied to zero, the result is defined to be one as a special case. ( i.e. 0! = 1 ) The function as applied to a positive integer n corresponds to the intuitive concept of counting the number of combinations n objects can make, by always using all n objects and ordering them in a line. There is a generalisation of the factorial function called the gamma function.

factorial series: One representation of the exponential function with base e (Euler's Number) shown as the sum of the infinite series

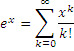
2. Alternatively, it describes the representation of Euler's Number through the sum of the series of reciprocals of successive factorials. ( i.e. the above case when x=1 )

factorisation: The process of representing a mathematical object as the product of two or more simpler objects of the same type.

factor theorem: A theorem that relates the roots of a polynomial to its factors. class="d-title" Namely, that ( x - a ) is a factor of the polynomial p(x) as long as a is a root of p(x). ( i.e. p(a)=0 ) The converse is also true though trivial. The Factor Theorem can be considered as a special case of the remainder theorem.

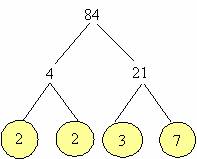
factor tree: A graphical representation usually for caluculation or representation of the prime factorisation of a positive integer. It can of course be used for factorisation of polynomials in a similar fashion, though this usage is relatively rare. The different routes that a positive is broken down means that different trees can be produced from a number, though the unique factorisation of integers into prime numbers guarantee that the numbers at the tip of all branches together form a unique set of prime factors. For this reason there's no reason why this graphical tool cannot be used for mathematical objects where unique factorisation does not exist.

Fahrenheit degree: A unit of temperature represented by the symbol ºF, which can be calculated from Celsius by multiplying 1.8 before adding 32.

fair game: A game in which, given symmetric parameters for the 2 players, is not biased towards either one of them.

false position, rule An iterative method in Numerical Analysis for finding the roots of a continuous function by evaluations of approximations (points known to be NOT the root), to any level of specified accuracy.

family: A set of related mathematical objects. e.g. A set of curves with the same form of equation differing in parameters, a set of transformation of the same type etc.

farad: The SI unit of capacitance, the charge a capacitor will take for a given potential across.

F-distribution: A continuous probability distribution of a random variable which is the ratio of two independent chi-square distributed variables, with each divided by its corresponding degree of freedom.

feasible region: The set of all points satisfying the system of linear inequalities in a linear programming problem.

femto-: SI prefix that means one one-quadrillionth (1/1 000 000 000 000 000).

Fermat numbers: A number of the form

The motivation behind this definition is that a prime number in the form 2^k+1 implies that k must itself be a power of 2.

Fermat's last theorem: A theorem in number theory only recently (1995) proven despite being proposed over 350 years ago (1637) and have subsequently received a lot of attention. It states that all solutions for the equation

xⁿ + yⁿ = zⁿ

where x, y, z and n are inetegers have the value of n as 1, 2 and 3 only.

Fibonacci sequence: A specific sequence defined by the rule that each number is (or "can be", if we're extending a sequence in both directions) calculated by the sum of the two terms before it and that the first two terms of the sequence (the terms indexed by 1 and 2) both take the value of 1. One interesting property amongst many, is that the ratio of each term to the next in this sequence approaches what is termed the golden ratio, as the index tends to infinity. This limit ( i.e. the golden ratio) can then be calculated by attempting to find the fixed point of the iterative formula through assuming that the 3 terms in the iterative formula are equal. (Hence, "fixed" point.) This yields a quadratic equation which actually produces 2 fixed points; the positive number is the golden ratio, while the negative number is what the ratio approaches as we extend the sequence towards an index of negative infinity.

field: An algebraic structure which generalises the concept and structure of the real numbers, it is a set of elements with certain operations defined obeying some specified rules.

finite group: A group with a finitely many elements.

finite sequence: A sequence with finitely many terms.

finite series: A series with finitely many many terms.

first-order convergence: The convergence of a sequence where the ratio of error between consecutive terms tends to a number between 0 and 1.

first-order differential equation: An equation that links a number of variables and the (first) derivatives of these variables with respect to the other variables.

first derivative test: A crude method for determining the nature of a stationary point. It works by checking the gradients of points on both sides of the stationary point (which has a gradient of zero by definition). If the signs are different, the stationary point is an extremum. While if the signs are the same, then it is an inflection point. The use of this method relies on the assumption that the gradients do not change signs between "the points of test" and the stationary point. This assumption may be hard to justify for more exotic functions.

five-number summary: Also known as a five-point summary. A conventional group of parameters shown in box-and-whisker plots in summary statistics. They can of course be shown in other ways or with additional parameters. The five numbers are: Q_0 the minimum, Q_1 the lower quartile, Q_2 the median, Q_3 the upper quartile and Q_4 the maximum. The provision of these summaries allow for a quick assessment or comparison of average (in this case, median), dispersion as well as skewness of the data.

fixed-point iteration: See iteration.

floor function: Usually written as . It is a function that always round the value down to the next closest integer unless it is already an integer. It is equivalently defined as the greatest integer that is not smaller than x. Though such a definition can be extended to any set with guaranteed infimum, it is usually defined for Real numbers only.

fluid mechanics: The study of fluids in applied mathematics: in motion, at rest and under forces.

fluxion: An archaic term for the derivative of a continuous function used by Newton.

focal chord: A chord that contains the focus of a conic section.

focal radius: Refers to the line segment between any point on a conic section and its focus. It can also refer to the length of such a line segment.

focus: A point which, together with a line called the directrix, defines the set of points which form a conic section.

foil method: A restrictive method that serves as a first point of introduction to the concept of expanding brackets. The mnemonic FOIL stands for First(s), Outside(s), Inside(s) and Last(s), referring to the four combinations to multiply out in the case of expanding two brackets each with two terms inside. Thus this method does not apply to cases when there are more than two brackets or when there are more than two terms in one of the brackets (e.g. a trinomial.).

foot: An imperial, pre SI unit of length, roughly 0.3 metres.

force: An inflience which causes the change in velocity of an object.

formula: An equation that is specifically written to solve a particular problem.

forward difference: A quantity expressed by the equation below. It is the unsigned difference between the value obtained from a specified argument, and the value obtained by adding a specified increment to the said argument.

The limit of the forward difference as h tends to zero is known as the derivative. Forward differences can also be used in obtaining function describing each term from sequences of numbers, such as in Newton's Forward Difference formula.

four-colour problem: A classic mathematical problem that was inspired by the number of colours needed so that adjacent countries always have different colours, no matter how the land is divided. The mathematical problem is essentially the same as that considered although some conditions are added, such as countries are only allowed connected land masses, so that two pieces of land not adjacent to each other cannot be forced to have the same colour by virtue that they belong to the same country, as is the case for Russia(St. Petersburg) and the United States(Alaska) in the real world.

This "problem" is now a theorem, having been proven in the 20th century. It was one of the first mathematical theorems to be proven by using a computer. The mathematicians essentially divided the problem into a number of cases (thousands, nonetheless a limited number) so that four colours was checked to be sufficient with each of these cases. The nature of the method of proof means that it was as controversial when it was published as it is now, due mainly to objection by some that such proofs essentially cannot be checked by a human.

Fourier series: An infinite series of the sine functions and cosine functions that aims to approximate periodic functions of more complex behaviour.

Very useful in physics and engineering. The Fourier coefficients, that is, the coefiicients of the above series can be found by

f.p.s.: Foot-pound-second. A system of units analogous to the system of centimetre-gram-second or the system with SI unitsmetre-kilogram-second. Somewhat outdated as imperial units are no longer the preferred units of choice by the scientific community.

fractal: A self-similar geometric shape consisting of parts which is the same as an enlargement of some of its parts.

fraction: A form of representation of a quantity as the result of division (quotient) of one quantity by another, where the dividend is placed on top (known as the numerator) and the divisor at the bottom (known as the denominator) with a horizontal line placed between the two. The numbers are usually required to be intergers with the denominator being non-zero, although decimal, other fractions or even algebraic expressions can be used as components of fractions.

fractional expression: An algebraic expression of a polynomial divided by another - also known as a rational expression.

frequency: The number of cycles or occurrences within a given interval (number) of a continuous (discrete) quantity..

frequency curve: A graphical representation of frequency information of observations through the use of a smooth curve.

frequency distribution: A function showing the number of instances in which a variable takes each of its possible values.

frequency function: The probability mass function of a discrete random variable or the probability density function of a continuous random vairable, with probability viewed as a long term relative frequency.

frequency polygon: A graphical representation of frequency information of observations through the use of a continuous piecewise-linear curve.

frequency table: An array of quantites representing frequency information (absolute or relative).

Fresnel integrals: The collective class="d-title" name of two transcendental functions defined by the integral of trigonometric functions, used in the study of optics.

friction: A motion resisting force due to contact of objects in relative motion.

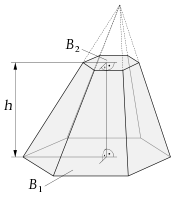
frustum: The shape of a solid figure formed by the the curved surface of a cone or the slanted surfaces of a pyramid, and two planes placed between the apex and the base, with both planes parallel to the base.

F-test: The collective class="d-title" name of a number of statistical tests where the test statistic under H₀ in the hypothesis testing is F-distributed.

fulcrum: A structure upon which a lever pivots.

function A specific type of mapping where there must be exactly one value (i.e. output) in the range for any arguments (i.e. inputs) within the allowed set of arguments (i.e. the domain).

Alternatively, A function is a set of ordered pairs where no two ordered pairs have the same first element.

functional series: A series where the individual terms are functions.

function of a complex variable: A function whose domain is a subset of the complex numbers while not a subset of the real numbers.

function of a function: 1. A composite function.

2. Operators of functions or other functions which takes functions as arguments - when the functions are considered as members of a vector space, such a function of a function can be known as a functional.

fundamental theorem of algebra: Analogous to the fundamental theorem of arithmetic, it is a theorem which states that all complex monic polynomials can be uniquely expressed as the product of a unique set of monic linear expressions.

The real number version, which states that all real monic polynomials can be uniquely expressed as the product of a unique set of irreducible polynomials, is also known as the fundamental theorem of algebra.

fundamental theorem of arithmetic: The theorem which states that all positive integers (apart from 1) can be expressed as the product of a unique set of prime numbers.

fundamental theorem of calculus: The theorem which states that differentiation and integration are opposite processes (or operations) of one another..