* Terms and Conditions apply.
When we face an important problem our eagerness to solve it often leads us to accept the first solution that comes to mind, so that we can implement it without delay. Very often this will not be the most effective solution available. The best approach, particularly with open-ended problems, is to create a range of possible solutions from which we can subsequently select the best.
These examples highlight two very common difficulties in finding the best solution to a problem:
1. Not seeing all the relationships between different parts of the problem.The human mind can focus on only a small amount of information at one time, so that we often find it difficult to hold a complete and detailed mental picture of a problem in our minds. Without this we may overlook important relationships.
It's vital to know how all the parts of a problem are interrelated, otherwise we can waste time and perhaps not find the most effective solution. For example, our solution may aggravate the problem because we overlooked a particular relationship, or there may be a better solution involving two aspects we didn't relate.
2. Not seeing beyond the most obvious solution.The way we associate ideas and concepts in our minds, forming patterns which are reinforced by experience, often makes it hard to see common situations in a new light. Relationships between information which are new or seem 'unlikely', and ideas which appear irrelevant, may be either consciously excluded or not triggered from memory because of their weak associations with the situation.
To find creative solutions to our problems we need to escape habitual ways of looking at situations.
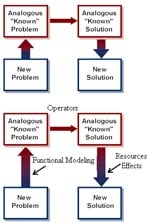
Using models to represent problems
Models give shape and structure to information, making it easier to remember, think about and build on our ideas. They can highlight gaps in our information, help to predict the consequences of our actions and stimulate ideas. Models are also invaluable for communicating problems and ideas for their solution to other people.
In most situations you will find it helpful to use a model to represent the parts of a problem in an appropriate pattern. There are many different types, composed variously of words, graphics, mathematical formulae, symbols, and so on, as well as physical models.
There are various standard models which can be used to represent problems which have common elements linked by the same relationships. These can be applied to any problem which fits the model. Chemical equations and algebraic formulae are examples. So are business games, which represent details of a variety of business situations and predict the consequences of our actions according to how aspects of those situations interact in the real world.
Another example is communication, where the common elements are the originator,. the sender, the message, the medium, and the receiver. Effective communication relies on an efficient flow of information from one end to the other.
This model can be used to analyse a situation and identify exactly what is happening at each stage which may be preventing effective communication.
In addition to standard models, there is a wide range of options for representing problems..
Words as models
Words are the simplest and one of the most popular and flexible ways of representing a problem, either alone or in combination with pictorial or graphical elements.
The easiest way to create a word model is to list the main features of a problem, perhaps including associated ideas that come to mind. This can be updated and expanded as you think of additional relevant information. Word models can be manipulated easily, reordering the words in sequence or classifying them into groups, to highlight the relationships arid differences between the information.
Abbreviated notes can be used effectively in the same way although prose, which is often used to describe a problem, is less effective. The more structure that exists in each descriptive unit, the less easy it is to add to and manipulate the information to reveal new relationships.
Words are easy to record and act as potent stimuli to the imagination. They are the most common way of communicating problems to other people. However, there are some drawbacks. The choice of a particular word or phrase to describe an idea can obscure its relationship with other relevant information. For example, if you use the word box to describe a 'container' you want to redesign it could narrow your thinking about different shapes and materials.
Also it is often difficult to give structure to the information contained in word models. Therefore it's a good idea not to use them alone, but perhaps as a preliminary' to creating other types of model.
Drawings and diagrams
Drawing is an ideal way of beginning to create some kind of structure with your ideas. Unlike words alone, lines can represent relationships more easily and give concrete form to a problem.
In making a drawing to represent a problem you are not trying to create a work of art. It should be spontaneous, like doodling, allowing your thoughts to evolve in a visual way. Drawings can suggest new relationships between ideas, new ways of structuring a problem and new routes to a solution.
A more structured form of drawing is to create a diagram.
Mind maps
This is a visual method of structuring ideas which can take on almost any form. The main idea or concept is written at the centre of a page and then any related ideas that spring to mind are added as branches off this central point. As each one triggers more ideas they are added as connecting lines, branching outwards in all directions.
Ideas are written in block capitals along a line as it is added, so that each one acts as a clear trigger to the recall of associated ideas. The method capitalises on the brain's power of association, subsequent branches becoming more and more remote from the central idea.
The process should be spontaneous. You must not consciously think about where to place branches, whether to exclude an idea, or try to think of ways of extending a particular branch if nothing springs to mind. The aim is to record everything you can recall which may have the remotest relationship with the central idea.
Chain diagrams
These are created in a more logical way than mind maps and show clearly how the main elements of a problem are related. For example, it could show the stages in the manufacture of a product or the supply of a service, with the labour, time or cost improvement at each stage.
Chain diagrams can be very complicated, with feedback loops and so on, showing the different kinds of relationships between information. The direction of 'flow' of the process can be represented by arrows and numbers can be added to quantify what is happening at each stage.
These diagrams can also be used to show the alternative choices that can be made in the system and the influence of chance events. This forms what is sometimes called a tree diagram. When numbers are added to show the value of alternative choices and the probability of chance events a decision tree is created, which can be used to evaluate alternative courses of action.
Force field diagrams
These are analytical tools for representing the dynamics of situations and suggesting ways of influencing the forces and pressures which create and maintain them. Creating a force field diagram involves identifying and representing graphically the equilibrium between two opposing sets of forces. The driving forces are those which would push the equilibrium in. the direction needed to achieve the objective. The opposing or restraining forces are those which act against the desired change - the obstacles to achieving the objective.
To push the equilibrium in the direction needed to achieve the objective you need to find ways of overcoming or neutralising the restraining or opposing forces, and/or strengthening the driving forces. Force field analysis can be divided into simple stages:
This technique is useful particularly where human factors are important, such as in behavioural problems and changes to working practices or systems.
Mathematical models
Problems which involve quantitative information need to be represented in mathematical terms, even if it is only to record the data. Mathematical models can represent the relationships between elements of a problem and provide a means of manipulating the information, eg a + b = c. In some situations they may be essential in finding an effective solution, eg in deciding what stress would be put on a newly designed turbine, before you can select an appropriate material for its manufacture.
Constructing simple mathematical models. is within everyone's ability, but some highly complex models are available now to the non-mathematician through personal computers. These can help to solve a large range of problems by analysing a situation and forecasting how various actions, changes or forces will affect it, eg financial modeling.
Representing problems and their possible solutions in quantitative terms is also a powerful way to persuade people, particularly those who think in an analytical way and favour 'hard facts' .
Using an appropriate model to represent a problem will often suggest some ideas for a solution. However, there are more powerful techniques for generating ideas.
Read the next article: The Road to a Solution - Generating ideas